9. Προβλήματα αρχικής τιμής

9.1. Διατύπωση του προβλήματος

Διαφορική εξίσωση ονομάζεται μία εξίσωση, ο οποία συσχετίζει μία ανεξάρτητη μεταβλητή \(x\), μία εξαρτημένη μεταβλητή \(y\) και τις παραγώγους της (\(y',y'',\dots\)). Η απαλοιφή των διαφορικών σε αυτή την εξίσωση είναι συχνά αδύνατη και γιαυτό έχουν αναπτυχθεί αριθμητικές μέθοδοι οι οποίες δεν αποκαλύπτουν την συνεχή λύση της \(y\), αλλά δίνουν αποτελέσματα σε συγκεκριμένα σημεία.

Στην φυσική και σε άλλες επιστήμες συναντάμε συχνά προβλήματα αρχικής τιμής, προβλήματα δηλαδή στα οποία είναι γνωστή μια αρχική κατάσταση και η διαφορική εξίσωση περιγράφει την μεταβολή της κατάστασης. Η ανεξάρτητη μεταβλητή είναι συνήθως ο χρόνος, χωρίς αυτό να είναι δεσμευτικό για τις μεθόδους που θα περιγραφούν παρακάτω.

Με δεδομένη λοιπόν την διαφορική εξίσωση και μια αρχική κατάσταση:

\[y'(t)=f(t,y(t)), \; y_0=y(t_0)\]

θα υπολογίσουμε την εξέλιξη στον χρόνο της συνάρτησης \(y(t)\).

Αναλυτικά η εξέλιξη της συνάρτησης υπολογίζεται με ολοκλήρωση της διαφορικής εξίσωσης.

Exercise 9.1

Το μεταβατικό ισοζύγιο ενέργειας του τοιχώματος ενός μεταλλικού μαγειρικού σκεύους δίνεται από την σχέση:

\[ m C_p \frac{dT}{dt}=-hA(T-T_a)\]

ή ισοδύναμα

\[ \frac{dT}{dt}=-\frac{1}{τ}(T-T_a) \]

με \(τ=\frac{mC_p}{hA}\), η σταθερά του χρόνου.

Η εξίσωση αυτή έχει προκύψει με την παραδοχή ότι η εξωτερική θερμική αντίσταση είναι αρκετά μεγαλύτερη από την εσωτερική ή ισοδύναμα ότι το σκεύος έχει ομοιόμορφη θερμοκρασία \(T\) σε όλο το πάχος του.

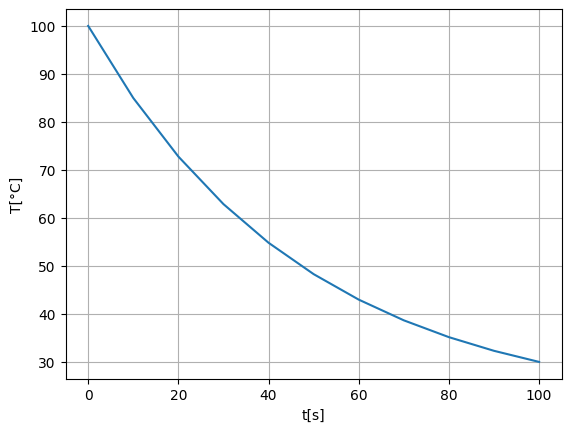
Αν η αρχική θερμοκρασία του σκεύους στον χρόνο 0s είναι 100°C, η θερμοκρασία του αέρα σταθερή στους 20°C και η σταθερά του χρόνου \(τ=41.8s\), υπολογίστε την εξέλιξη της θερμοκρασίας και την χρονική στιγμή που θα η θερμοκρασία του σκεύους θα φτάσει στους 40°C.

Η αναλυτική επίλυση είναι αρκετά απλή σε αυτό το πρόβλημα. Με μια απλή αναδιάταξη:

\[\frac{dT}{T-T_a}=-\frac{dt}{τ}\]

και τελικά

\[Τ=T_a+(T_0-Τ_a)e^{-\frac{t}{τ}}\]

import numpy as np
import matplotlib.pyplot as plt

dt=10   #s
tau=48.1    #s
Ta=20   #°C
T0=100  #°C
n=10

T=np.empty(n+1)
t=np.arange(0,(n+1)*dt,dt)

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t,Ta+(T0-Ta)*np.exp(-t/tau),"-")
ax.grid()

plt.show()

Στην αριθμητική ολοκλήρωση ξεκινάμε από την αρχική κατάσταση \((t_i,y_i)\) και υπολογίζουμε προσεγγιστικά την καινούργια κατάσταση \((t_{i+1},y_{i+1})\) κάνοντας ένα μικρό βήμα στην ανεξάρτητη μεταβλητή. Η διαδικασία αυτή εφαρμόζεται επαναληπτικά και έτσι μπορεί να προκύψει η εξέλιξη για το διάστημα που επιθυμούμε. Για τον υπολογισμό της καινούργιας κατάστασης είναι απαραίτητη η χρήση παραδοχών, η επιλογή των οποίων χαρακτηρίζει τις μεθόδους που θα συζητηθούν παρακάτω.

9.2. Μέθοδος Euler

Σύμφωνα με την μέθοδο Euler, θεωρούμε ότι η πρώτη παράγωγος παραμένει αμετάβλητη κατά την διάρκεια ενός βήματος από το \(t_{i}\) σε \(t_{i+1}\). Έτσι μπορεί να υπολογιστεί η καινούργια κατάσταση ως:

\[y_{i+1}=y_{i}+y'(t_{i+1}-t_i)\]

αρκεί να υπολογιστεί η παράγωγος \(y'\) από την σχέση \(y'(t)=f(t,y(t))\). Για τον υπολογισμό της παραγώγου μπορεί να χρησιμοποιηθεί το σημείο \(t_i\), το \(t_{i+1}\) ή κάποιο ενδιάμεσο.

9.2.1. Ρητή μέθοδος

Στην ρητή μέθοδο, η σταθερή παράγωγος \(y'\) υπολογίζεται στην αρχή του βήματος, δηλαδή στο \(t_i\). Καθώς το \(y(t_i)\) είναι ήδη γνωστό η σχέση \(y'(t)=f(t,y(t))\) μπορεί να εφαρμοστεί άμεσα, εξού και το όνομα της μεθόδου.

Exercise 9.2

Επιλύστε την Άσκηση 9.1 με την ρητή μέθοδο και βήμα Δt=10s. Συγκρίνετε γραφικά τα αποτελέσματα με την αναλυτική λύση.

import numpy as np
import matplotlib.pyplot as plt

dt=10   #s
tau=48.1    #s
Ta=20   #°C
T0=100  #°C
n=10

T=np.empty(n+1)
t=np.empty(n+1)

T[0]=T0
t[0]=0
for i in range(n):
    dydx=-1/tau*(T[i]-Ta)
    T[i+1]=T[i]+dydx*dt
    t[i+1]=t[i]+dt

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t,Ta+(T0-Ta)*np.exp(-t/tau),"-", label="Analytical")
ax.plot(t,T,"--o",label="Explicit")
plt.legend()
ax.grid()

plt.show()

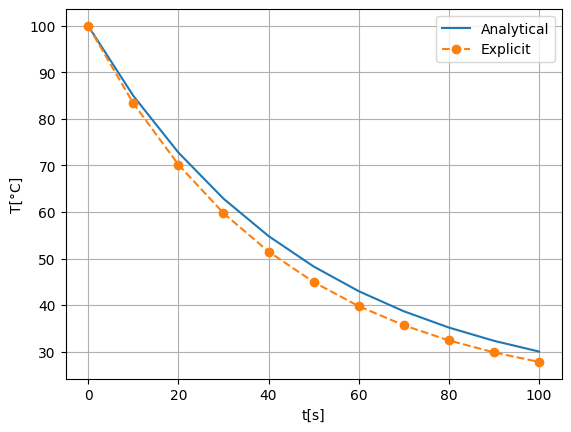
Παρατηρούμε ότι το σφάλμα μεγαλώνει καθώς απομακρυνόμαστε από την αρχική κατάσταση. Η ρητή μέθοδος είναι εύκολη στη εφαρμογή, αλλά είναι ευσταθής υπό την συνθήκη.

\[\left|1+Δt\frac{\partial f}{\partial y} \right|<1\]

9.2.2. Άρρητη μέθοδος

Στην αρρητή ή πεπλεγμένη μέθοδο, η σταθερή παράγωγος \(y'\) υπολογίζεται στο τέλος του βήματος (\(t_{i+1}\)), δηλαδή \(y'=f(t_{i+1},y(t_{i+1}))\) και επομένως πρέπει να λυθεί αλγεβρικά η (άρρητη) εξίσωση:

\[y_{i+1}=y_{i}+f(t_{i+1},y(t_{i+1}))(t_{i+1}-t_i)\]

Exercise 9.3

Επιλύστε την Άσκηση 9.1 με την αρρητή μέθοδο και βήμα Δt=10s. Συγκρίνετε γραφικά τα αποτελέσματα με την αναλυτική λύση και την ρητή μέθοδο.

\[T_{i+1}=T_{i}+\left(-\frac{T_{i+1}-T_a}{τ}\right)Δt \]

\[T_{i+1}=\frac{T_i+\frac{Δt}{τ}T_a}{1+\frac{Δt}{τ}}\]

import numpy as np
import matplotlib.pyplot as plt

dt=10   #s
tau=48.1    #s
Ta=20   #°C
T0=100  #°C
n=10

Texp=np.empty(n+1)
Timp=np.empty(n+1)
t=np.empty(n+1)

Texp[0]=T0
Timp[0]=T0
t[0]=0.
for i in range(n):
    dydx=-1/tau*(Texp[i]-Ta)
    Texp[i+1]=Texp[i]+dydx*dt
    Timp[i+1]=(Timp[i]+dt/tau*Ta)/(1+dt/tau)
    t[i+1]=t[i]+dt

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t,Ta+(T0-Ta)*np.exp(-t/tau),"-", label="Analytical")
ax.plot(t,Texp,"--o",label="Explicit")
ax.plot(t,Timp,"--*",label="Implicit")
plt.legend()
ax.grid()

plt.show()

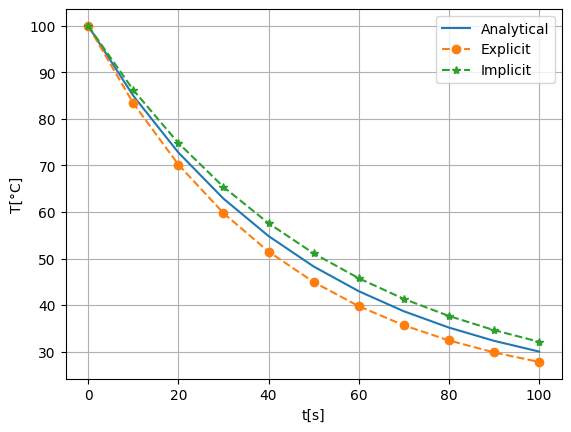
Η άρρητη μέθοδος είναι πιο δύσκολη στην εφαρμογή και γιαυτό δεν είναι η πρώτη επιλογή όταν χρειαζόμαστε γρήγορα αποτελέσματα.

Έχει όμως το πλεονέκτημα της ευστάθειας χωρίς συνθήκες, που σημαίνει ότι μπορεί να χρησιμοποιηθεί σε απλές και δύσκαμπτες διαφορικές εξισώσεις. Επίσης συγκλίνει με μεγαλύτερα χρονικά βήματα από την ρητή μέθοδο. Σε κάθε περίπτωση ο έλεγχος της ακρίβειας των αποτελεσμάτων είναι απαραίτητος.

9.2.3. Crank-Nicholson

9.3. Μέθοδος Runge-Kutta

9.4. Ειδικές περιπτώσεις

Μπορούμε να έχουμε περισσότερες από μία ανεξάρτητες μεταβλητές (π.χ. \(x,y,z,t\)).

Όταν έχουμε περισσότερες από μία εξαρτημένες μεταβλητές, χρειαζόμαστε και αντίστοιχο πλήθος διαφορικών εξισώσεων. Ένα σύστημα διαφορικών εξισώσεων μπορεί να λυθεί με τις μεθόδους που περιγράφηκαν παραπάνω.

Exercise 9.4

Επιλύστε το παρακάτω σύστημα διαφορικών εξισώσεων:

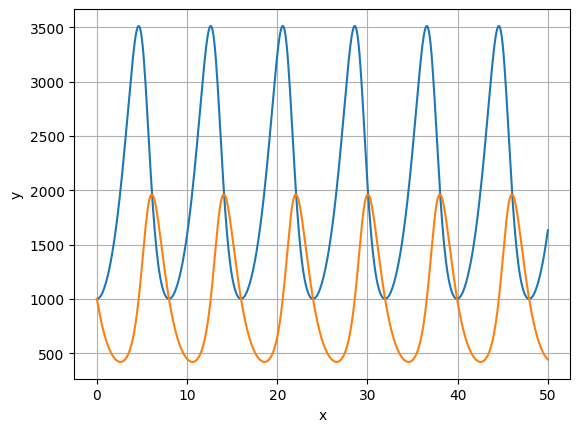
Για την προσομοίωση ενός οικοσυστήματος με ένα θήραμα (πληθυσμός \(Ν_0\)) και ένα θηρευτή (πληθυσμός \(Ν_1\)) μπορεί να χρησιμοποιηθεί το μοντέλο Lotka-Volterra. Οι ετήσιοι ρυθμοί μεταβολής των πληθυσμών δίνονται από τις διαφορικές εξισώσεις:

\[\begin{split} \begin{aligned} \frac{dN_0}{dt}&=&0.67 N_0&-& 0.67\cdot 10^{-3} N_0 N_1\\ \frac{dN_1}{dt}&=& N_1 &+& 0.5\cdot 10^{-3} N_0 N_1 \end{aligned} \end{split}\]

Ο αρχικός πληθυσμός του θηράματος και του θηρευτή είναι 1000 άτομα. Χρησιμοποιώντας την συνάρτηση solve_ivp υπολογίστε την εξέλιξη των πληθυσμών για διάστημα 50 ετών και απεικονίστε τα αποτελέσματα σε γράφημα.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def  dNdt(t,N):
    dN0dt= 0.67*N[0]-0.67e-3*N[0]*N[1]
    dN1dt= -1.0*N[1]+0.5e-3*N[0]*N[1]
    return np.array([dN0dt,dN1dt])

sol = solve_ivp (dNdt, [0,50], [1000, 1000],method="RK45",max_step=0.1)    # RK45 = Runge Kutta of order 4 (default)
print(sol)

fig, ax = plt.subplots()
ax.set(xlabel='x', ylabel='y')
ax.plot(sol.t,sol.y[0]) 
ax.plot(sol.t,sol.y[1]) 
ax.grid()
plt.show()

  message: The solver successfully reached the end of the integration interval.
  success: True
   status: 0
        t: [ 0.000e+00  1.000e-01 ...  4.990e+01  5.000e+01]
        y: [[ 1.000e+03  1.002e+03 ...  1.572e+03  1.632e+03]
            [ 1.000e+03  9.513e+02 ...  4.501e+02  4.413e+02]]
      sol: None
 t_events: None
 y_events: None
     nfev: 3002
     njev: 0
      nlu: 0