8. Παραγώγιση#
8.1. Διατύπωση του προβλήματος#
Πολλές φορές χρειάζεται να εξάγουμε την παράγωγο (πρώτη ή μεγαλύτερη) ενός μεγέθους \(y\) από δεδομένα μετρήσεων ή υπολογισμών σε διακριτά σημεία. Για αρχή θα υποθέσουμε ότι τα διακριτά σημεία έχουν σταθερή απόσταση \(h\) μεταξύ τους.
\(x\) |
\(f(x)\) |
|---|---|
\(\dots\) |
\(\dots\) |
\(x_i-h\) |
\(f(x_i-h)\) |
\(x_i\) |
\(f(x_i)\) |
\(x_i+h\) |
\(f(x_i+h)\) |
\(\dots\) |
\(\dots\) |
Στόχος μας είναι η εκτίμηση των παραγώγων της \(f(x)\) σε όλο το πεδίο των \(x\). Ο μαθηματικός ορισμός της πρώτης παραγώγου στο σημείο \(x_i\) είναι:
8.2. Εκτίμηση πρώτης παραγώγου με εμπρός και πίσω διαφορές#
Με την χρήση της σειρά Taylor μπορεί να υπολογιστεί η \(f(x)\) σε οποιοδήποτε σημείο, εφόσον γνωρίζουμε όλες τις παραγώγους στο \(x_i\):
Εφαρμόζοντας τον ορισμό στα σημείο \(x_{i+1}\) και αποκόπτοντας τον τρίτο όρο και τους ακόλουθους
προκύπτει η σχέση εκτίμησης παραγώγου με εμπρός διαφορές (forward difference):
Με παρόμοιο τρόπο προκύπτει η εκτίμηση παραγώγου με πίσω διαφορές (backward difference):
8.3. Εκτίμηση πρώτης παραγώγου με κεντρικές διαφορές#
Μια καλύτερη προσέγγιση παίρνουμε αν κρατήσουμε τον τρίτο όρο και χρησιμοποιήσουμε και τις δύο σειρές Taylor:
Αφαιρώντας κατά μέλη, προκύπτει η σχέση εκτίμησης παραγώγου κεντρικών διαφορών (central difference):
η οποία έχει μια τάξη μεγέθους μικρότερο σφάλμα. Με χρήση περισσότερων όρων της σειράς Taylor προκύπτουν σχέσεις, οι οποίες απαιτούν μεν περισσότερα σημεία, δίνουν δε πιο ακριβή αποτελέσματα.
Exercise 8.1
Τα Προηγμένα Συστήματα Υποβοήθησης Οδηγού (ADAS) χρησιμοποιούν αισθητήρες απόστασης για την εκτίμηση της κινηματικής των οχημάτων στο δρόμο. Για τις ανάγκες της άσκησης δημιουργείστε έναν τεχνητό πίνακα δεδομένων με χρόνο από 0 έως 10s και χρονικό βήμα 0.1s. Η απόσταση θα υπολογιστεί από την σχέση:
Όπου
t ο χρόνος σε s
s η απόσταση σε m
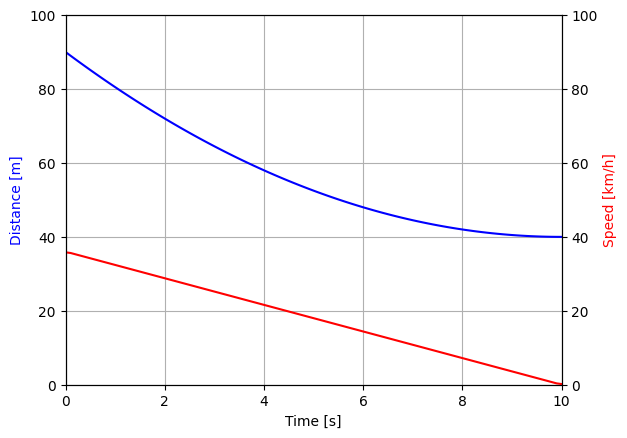
Υπολογίστε την απόσταση και την ταχύτητα και παρουσιάστε τα αποτελέσματα σε γράφημα.
import numpy as np
import matplotlib.pyplot as plt
tend = 10 # seconds
dt = 0.1 # seconds
time = np.arange(0, tend + dt, dt)
n = time.size # number of data points
distance = 90 - 10 * time + 0.5 * time**2
velocity = np.empty(n)
velocity[0] = (distance[1] - distance[0]) / dt # forward difference
for i in range(1, n - 1):
velocity[i] = (distance[i + 1] - distance[i - 1]) / (2 * dt) # central difference
velocity[-1] = (distance[-1] - distance[-2]) / dt # backward difference
fig, ax = plt.subplots()
ax.set(xlabel="Time [s]")
ax.set_ylabel("Distance [m]", color="b")
ax.plot(time, distance, "-b")
ax.set_ylim(bottom=0, top=100)
ax2 = ax.twinx()
ax2.set_ylabel("Speed [km/h]", color="r")
ax2.plot(time, abs(velocity) * 3.6, "-r")
ax2.set_ylim(bottom=0, top=100)
plt.xlim(0, tend)
ax.grid()
plt.show()
Η συνάρτηση numpy.gradient χρησιμοποιείται για εκτίμηση της πρώτης παραγώγου σε μια σειρά σημείων εφαρμόζοντας κεντρικές διαφορές στα εσωτερικά σημεία και εμπρός και πίσω διαφορές στα εξωτερικά.
Exercise 8.2
Χρησιμοποιήστε την numpy.gradient για τον υπολογισμό της ταχύτητας στην Άσκηση 8.1 και επαληθεύστε ότι ταυτίζονται με τα αποτελέσματα του κωδικά μας με ανοχή σχετικού σφάλματος \(10^8\).
import numpy as np
import matplotlib.pyplot as plt
tend = 10 # seconds
dt = 0.1 # seconds
time = np.arange(0, tend + dt, dt)
n = time.size # number of data points
distance = 90 - 10 * time + 0.5 * time**2
velocity = np.empty(n)
velocity[0] = (distance[1] - distance[0]) / dt # forward difference
for i in range(1, n - 1):
velocity[i] = (distance[i + 1] - distance[i - 1]) / (2 * dt) # central difference
velocity[-1] = (distance[-1] - distance[-2]) / dt # backward difference
velocity2 = np.gradient(distance, time)
print(np.allclose(velocity, velocity2, rtol=1e-8))
True
8.4. Εκτίμηση παραγώγων ανώτερης τάξης#
Για την εκτίμηση της δεύτερης παραγώγου αθροίζονται οι παρακάτω σειρές Taylor:
Μετά από ορισμένους μαθηματικούς χειρισμούς προκύπτει:
Στα εξωτερικά σημεία προκύπτει με αντίστοιχο τρόπο:
Προσέξτε ότι η σχέση που προκύπτει είναι όμοια με αυτή που μας δίνουν οι πεπερασμένες διαφορές (όταν έχουμε ίσα διαστήματα \(h\)):
Η υλοποίηση numpy.diff δέχεται ένα διάνυσμα \(m\) τιμών \(f(x)\) και την τάξη \(n\) και επιστρέφει ένα διάνυσμα \(m-n\) τιμών που αντιστοιχούν στις πεπερασμένες διαφορες \(n\) τάξης . Ενδείκνυται επομένως για τον υπολογισμό των εσωτερικών σημείων.
Εκτός από την απευθείας εφαρμογή των παραπάνω σχέσεων μπορεί να χρησιμοποιηθεί η gradient δύο φορές, λαμβάνοντας υπόψη ότι η διαχείριση των ακραίων σημείων μπορεί να ενέχει σφάλματα.
Exercise 8.3
Υπολογίστε την επιτάχυνση στα δεδομένα της Άσκησης 8.1 με τις μεθόδους που προαναφέρθηκαν και παρουσιάστε τα αποτελέσματα σε πίνακα. Χρησιμοποιήστε χρονικό βήμα \(1s\).
import numpy as np
import matplotlib.pyplot as plt
tend = 10 # seconds
dt = 1.0 # seconds
time = np.arange(0, tend + dt, dt)
n = time.size # number of data points
distance = 90 - 10 * time + 0.5 * time**2
acceleration = np.empty(n)
acceleration[0] = (
distance[0] - 2 * distance[1] + distance[2]
) / dt**2 # forward difference
for i in range(1, n - 1):
acceleration[i] = (
distance[i + 1] - 2 * distance[i] + distance[i - 1]
) / dt**2 # central difference
acceleration[-1] = (
distance[-3] - 2 * distance[-2] + distance[-1]
) / dt**2 # backward difference
acceleration2=np.diff(distance,2)/dt**2
acceleration3=np.gradient(np.gradient(distance,time),time)
print(len(acceleration),acceleration)
print(len(acceleration2),acceleration2)
print(len(acceleration3),acceleration3)
11 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
9 [1. 1. 1. 1. 1. 1. 1. 1. 1.]
11 [0.5 0.75 1. 1. 1. 1. 1. 1. 1. 0.75 0.5 ]
8.5. Ειδικές περιπτώσεις#
Η ανάλυση που παρουσιάστηκε παραπάνω μπορεί να επεκταθεί και σε ανομοιόμορφα διαστήματα. Οι έτοιμες συναρτήσεις στις μονάδες κώδικα της Python υποστηρίζουν αυτή την λειτουργία, καθώς δεχονται όλο το διάνυσμα \(x\) ως όρισμα.
Σε ορισμένα προβλήματα τα δεδομένα χαρακτηρίζονται από θόρυβο, δηλαδή τυχαία σφάλματα. Για παράδειγμα πολλές φορές τα δεδομένα των μετρήσεων έχουν συχνά περιορισμένη ακρίβεια. Ο θόρυβος εξασθενεί με την ολοκλήρωση καθώς τα σφάλματα αλληλοαναιρούνται, αλλά ενισχύεται με την παραγώγιση. Στην τελευταία περίπτωση εφαρμόζονται τεχνικές προσαρμογής ελαχίστων τετραγώνων.
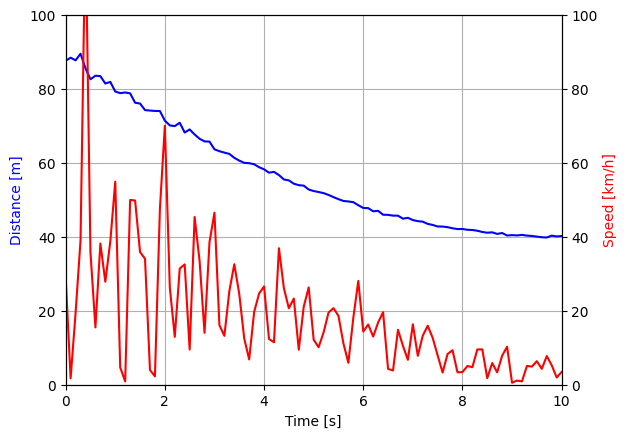
Exercise 8.4
Υπολογίστε την ταχύτητα στα δεδομένα της Άσκησης 8.1 εισάγοντας ένα μειούμενο τυχαίο σφάλμα \(E_s\) με την γεννήτρια τυχαίων αριθμών κανονικής κατανομής numpy.random.normal. Χρησιμοποιήστε την προεπιλεγμένη τυπική απόκλιση (scale=1) και μηδενική μέση τιμή (loc=0.0) για τον υπολογισμό του \(p\) στην ακόλουθη σχέση:
import numpy as np
import matplotlib.pyplot as plt
tend = 10 # seconds
dt = 0.1 # seconds
time = np.arange(0, tend + dt, dt)
n = time.size # number of data points
distance = (
90 - 10 * time + 0.5 * time**2 + 2 / (time + 1) * np.random.normal(size=time.size)
)
velocity = np.gradient(distance, time)
fig, ax = plt.subplots()
ax.set(xlabel="Time [s]")
ax.set_ylabel("Distance [m]", color="b")
ax.plot(time, distance, "-b")
ax.set_ylim(bottom=0, top=100)
ax2 = ax.twinx()
ax2.set_ylabel("Speed [km/h]", color="r")
ax2.plot(time, abs(velocity) * 3.6, "-r")
ax2.set_ylim(bottom=0, top=100)
plt.xlim(0, tend)
ax.grid()
plt.show()